알고리즘 - DFS/BFS

DFS / BFS

그래프

DFS, BFS 문제를 풀기 위해서는 그래프에 대해 이해하여야 합니다.

그래프는 노드와 간선으로 표현되며, 노드 == 정점과 같은 말입니다.

노드와 간선을 이해하기 위해서는 다음과 같은 그림을 보시면 도움이 됩니다.

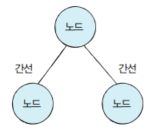
노드와 간선이 연결되어 있어야 인접할수 있습니다.

그래프를 표현하는 방식은 아래와 같이 두가지 방식으로 표현됩니다.

• 인접 행렬: 2차원 배열로 그래프의 연결 관계를 표현하는 방식
• 인접 리스트: 리스트로 그래프의 연결관계를 표현하는 방식

문제를 통해 해당 그래프를 그려볼 수 있습니다.

# 백준 1260 문제 예시
입력
첫째 줄에 정점의 개수 N(1 ≤ N ≤ 1,000), 간선의 개수 M(1 ≤ M ≤ 10,000), 탐색을 시작할 정점의 번호 V가 주어진다. 다음 M개의 줄에는 간선이 연결하는 두 정점의 번호가 주어진다. 어떤 두 정점 사이에 여러 개의 간선이 있을 수 있다. 입력으로 주어지는 간선은 양방향이다.

4(정점의 개수) 5(간선의 개수) 1(시작점)
1 2
1 3
1 4
2 4
3 4

1 - 2
| \ |
3 - 4

인접 행렬
    1  2  3  4
   -----------
1 | 0  1  1  1
2 | 1  0  0  1
3 | 1  0  0  1
4 | 1  1  1  0

인접 리스트
1 | 2 -> 3 -> 4
2 | 4
3 | 4

	인접행렬	인접리스트
메모리	메모리 사용량 높음	메모리 사용량이 적음
속도	정보를 얻는 속도가 빠름	순회하면서 조회
예시	graph[1] [4] == true	1| 2 -> 3 -> 4
시간복잡도	O(N²)	O(N+E)

DFS(Depth-First Search)

DFS는 깊이우선탐색으로 그래프에서 깊은 부분을 우선적으로 탐색하는 알고리즘입니다.

최대한 깊이 내려간 뒤, 더이상 깊이 갈곳이 없을 경우 옆으로 이동합니다.

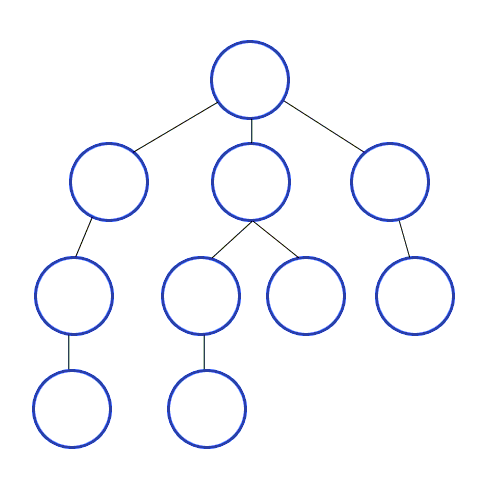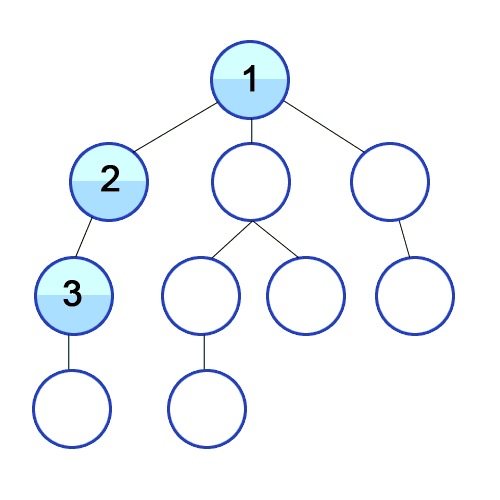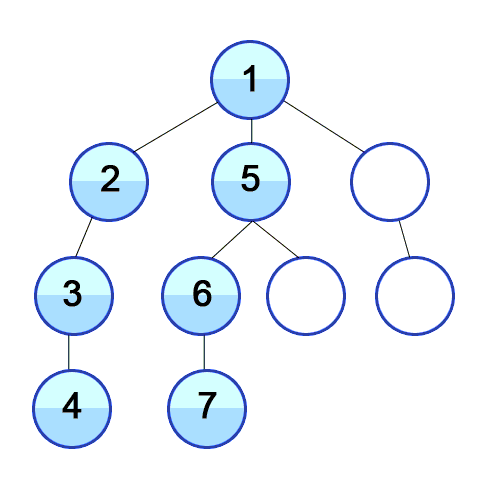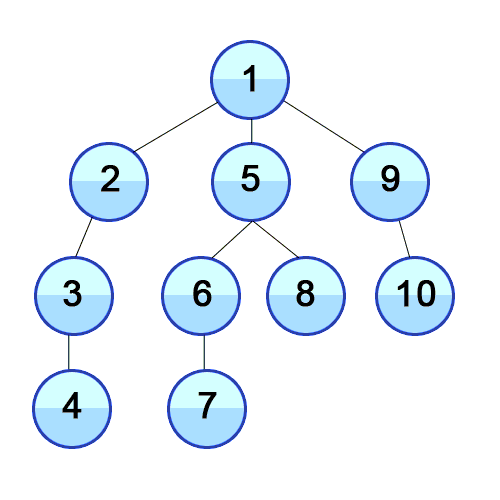
출처 https://developer-mac.tistory.com/64

• 모든 노드를 방문하고자 하는 경우에 이 방법을 선택함

• 깊이 우선 탐색(DFS)이 너비 우선 탐색(BFS)보다 좀 더 간단함

• 검색 속도는 너비 우선 탐색(BFS)에 비해서 느림

동작과정

1. 탐색 시작 노드를 스택에 삽입하고 방문 처리를 한다.
2. 스택의 최상단 노드에 방문하지 않은 인접 노드가 있으면 그 인접 노드를 스택에 넣고 방문 처리를 한다. 방문하지 않은 인접 노드가 없으면 스택에서 최상단 노드를 꺼낸다.
3. 2번의 과정을 더 이상 수행할 수 없을 떄까지 반복한다.

BFS(Breadth-First Search)

BFS는 넓이우선탐색으로 가까운 노드부터 탐색하는 알고리즘입니다.

최대한 넓게 이동한 다음, 더 이상 갈 수 없을 때 아래로 이동합니다.

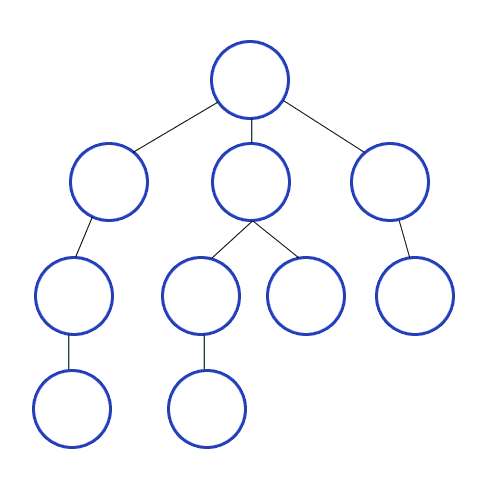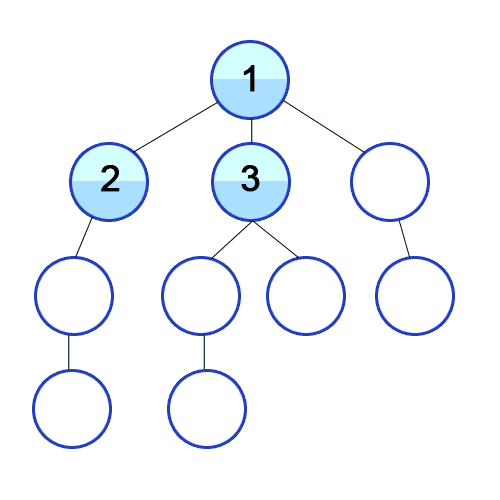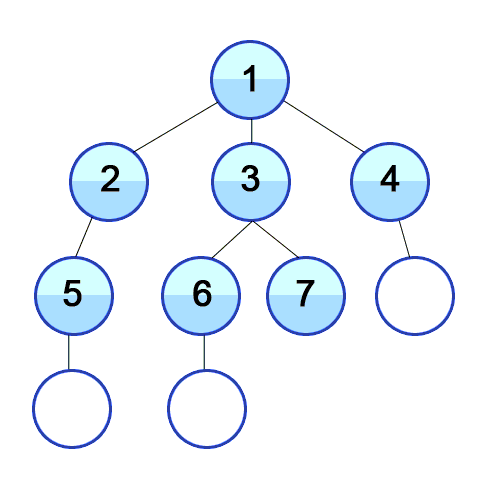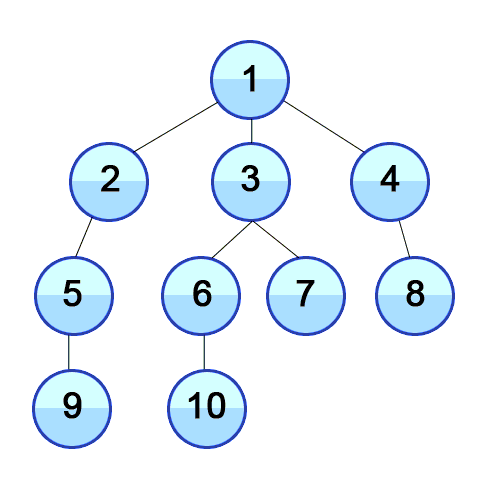
출처 https://developer-mac.tistory.com/64

• 두 노드 사이의 최단 경로를 찾고 싶을 때 선택함

동작방식

1. 탐색 시작 노드를 큐에 삽입하고 방문 처리를 한다.

2. 큐에서 노드를 꺼내 해당 노드의 인접 노드 중에서 방문하지 않은 노드를 모드 큐에 삽입하고 방문 처리를 한다.
3. 2번의 과정을 더 이상 수행할 수 없을때까지 반복한다.

비교

DFS(깊이우선탐색)	BFS(너비우선탐색)
현재 정점에서 갈 수 있는 점들까지 들어가면서 탐색	현재 정점에 연결된 가까운 점들부터 탐색
스택	큐

문제풀이

from collections import deque


def dfs(graph, v, visited):
    visited[v] = True
    for i in graph[v]:
        if not visited[i]:
            dfs(graph, i, visited)
            print(i)


def bfs(graph, v, visited):
    q = deque([v])
    visited[v] = True
    while q:
        pos = q.popleft()
        for i in graph[pos]:
            if not visited[i]:
                visited[i] = True
                q.append(i)
                print(i)


graph = [
    [],
    [2, 3, 8],
    [1, 7],
    [1, 4, 5],
    [3, 5],
    [3, 4],
    [7],
    [2, 6, 8],
    [1, 7],
]

visited = [False] * 9

dfs(graph, 1, visited)
bfs(graph, 1, visited)